Mathematik

Der Kosinus-Satz   Beweis des Kosinussatzes: siehe weiter unten

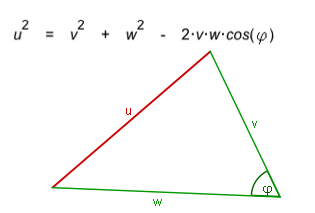Anwendungen des Kosinussatzes:

Sind von einem Dreieck alle drei Seitenlängen bekannt, so notieren Sie zuerst den Kosinussatz für diejenige Seite, welche dem gesuchten Winkel gegenüber liegt. Lösen Sie diese Gleichung nach dem Cosinus des gesuchten Winkels auf. Aus diesem Kosinuswert erhalten Sie den gesuchten Winkel mit dem Arcus-Cosinus.
Sind von einem Dreieck zwei Seiten und deren Zwischenwinkel bekannt, so liefert der Kosinussatz direkt die dritte Seite (bzw. das Quadrat dieser Seite).
Sind von einem Dreieck zwei Seiten und ein anliegender Winkel (≠ Zwischenwinkel) bekannt, so notieren Sie zuerst den Kosinussatz für diejenige Seite, welche dem bekannten Winkel gegenüber liegt. Diese Gleichung ist eine quadratische Gleichung für die dritte Dreiecksseite. Diese Gleichung lösen Sie mit einem Solver oder mit der Lösungsformel für quadratische Gleichungen.

Beweis des Kosinussatzes:

Der folgende hübsche (dynamische) Beweis von Dmitrij Nikolenkov setzt bloss Ähnlichkeit und den Kosinus am rechtwinkligen Dreieck voraus:
Verwenden Sie die Steuerungselemente unter der Abbildung (um die einzelnen Beweisschritte zu sehen)

Das ist ein mit GeoGebra www.geogebra.org erstelltes Java-Applet. Möglicherweise ist Java auf Ihrem Computer nicht installiert; bitte besuchen Sie in diesem Fall www.java.com

Erstellt von Dmitrij Nikolenkov mit GeoGebra